Does AI Tutoring Work? Size Matters
A First Introduction to Effect Size
Sal Khan's Khanmigo was first to market with AI-tutoring, and early reports suggest uptake in K-12. But how do we know if it really works? More importantly, how would we measure its effectiveness? Welcome to the world of effect sizes.
Consider a recent study by Harvard University researchers claiming that "students learn more than twice as much in less time with an AI tutor compared to an active learning classroom, while also being more engaged and motivated." The researchers developed their own AI tutor based on generative AI, and their findings are striking. Buried in the technical details was the key insight: "The analysis revealed a statistically significant difference (z = -5.6, p < 10^-8)" with "an effect size in the range of 0.73 to 1.3 standard deviations."
This last number – the effect size – is the crucial piece. Yet surprisingly, many research studies still report only "statistical significance" instead of effect sizes and confidence intervals. The Harvard study's large effect size is particularly noteworthy, as such magnitudes are rare in educational research. But effect sizes matter regardless of their magnitude, for two key reasons: science builds on cumulative evidence rather than single studies, and even small effects can have substantial real-world impact depending on context.
What is Effect Size?
We live in a world of causes: how some thing affects some other thing. In other words, we want to know the effect of X on Y.
What are some examples of these cause-effect relationships in the real-world:
The effect of a treatment on some outcome, like how a new medication impacts blood pressure levels in patients with hypertension, or how cognitive behavioral therapy influences depression symptoms over time
The effect of vaccines on disease transmission rates in a population, including both direct protection for vaccinated individuals and indirect protection through reduced community spread of the pathogen
The effect of educational interventions on student learning outcomes, such as how introducing a new math curriculum impacts test scores and long-term mathematical understanding
The effect of monetary policy decisions on economic indicators, like how changes in interest rates influence inflation rates, employment levels, and consumer spending patterns
The effect of environmental regulations on air quality metrics, including how emissions standards for vehicles and industry affect particulate matter levels and respiratory health in urban areas
The effect of social media usage on mental health indicators, such as how time spent on platforms correlates with reported anxiety levels, sleep quality, and social connection
The important thing here is that we want to know not only what causes the effect Y, but the size or magnitude of the effect. That in a nutshell is effect size. As Paul D. Ellis, who wrote “the book” on effect sizes, notes: “I am sometimes asked, what do researchers do? The short answer is that we estimate the size of effects.”1
Let’s define our terms precisely:
An effect is the outcome or change in Y brought about by X.
An effect size measures the magnitude of this outcome in Y.
Unfortunately, most research studies in the social sciences continue to report “statistical significance” (p-values) and statistics textbooks inundate students with obscure details about hypothesis testing (p-values again). Statistical significance is important but it pales in significance to effect sizes. A p value might tell us the direction of an effect, but only an estimate of effect size tells how big it is. We should always start with effect sizes.
Effect Sizes in Action: An Educational Case Study
Imagine you're a school principal evaluating two different reading programs (let's call them Program A and Program B) to help struggling readers in your school. You run a study with 200 students split between the two programs.
After analyzing the data, you get these two key pieces of information:
Statistical Significance (p-value): You find that Program A performed "better" than Program B with p < 0.05. This tells you that the difference between programs is probably not due to random chance. But here's the crucial part - it doesn't tell you how much better Program A was.
Effect Size: When you look at the effect size, you discover that students in Program A improved their reading scores by approximately 0.2 grade levels more than Program B students over the school year.
Now comes the important interpretation:
The p-value (statistical significance) tells you "Yes, Program A is probably better than Program B"
But the effect size tells you much more "Program A leads to 0.2 grade levels of additional improvement"
As a principal making a real decision, the effect size is far more important. Even though Program A is "statistically significantly better," an improvement of 0.2 grade levels might be too small to justify switching programs, especially if Program A is more expensive or requires more resources to implement.
This example illustrates why focusing only on "statistical significance" can be misleading in practice. You need to know not just if there's an effect, but how big that effect is to make informed decisions.
Measuring Effect Size: A Practical Example
Let's explore effect sizes with a detailed example. Imagine you're evaluating an after-school tutoring program with:
Treatment group: 100 students receiving tutoring
Control group: 100 students following their regular schedule
Both groups taking the same standardized math test
Both groups starting with similar abilities
After a semester, the data shows:
Treatment Group (With Tutoring):
Average score: 74
Standard deviation: 15
Control Group (No Tutoring):
Average score: 69
Standard deviation: 15
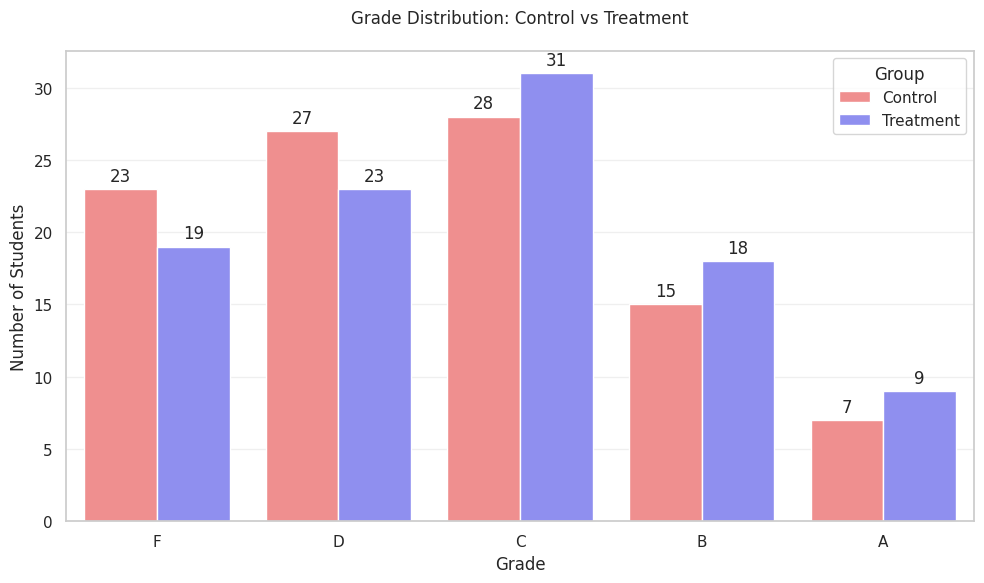
Figure 1 shows the results of the experiment in the form of bar chart and a distribution graph.
By just looking at the raw numbers, we can see the tutoring group scored 5 points higher on average. But is 5 points a lot or a little? That’s the key question. This is where calculating the effect size will help us understand the practical significance of this difference.
Calculating the Effect Size
Once we have the data, it’s straightforward to calculate the effect size. There are different ways of calculating effect sizes, depending on the data and the discipline. But we will set that aside for now. Our goal is to get an overview of what the process entails. We will use one of the most common methods, called Cohen’s d. To calculate Cohen’s d, we need the the means and standard distributions of our two groups.
First, the formula for Cohen's d is:
d = (Mean of Group 1 - Mean of Group 2) / Pooled Standard Deviation
From our data:
Tutoring Group (Group 1) Mean = 74
No Tutoring (Group 2) Mean = 69
Standard Deviation for both groups = 15
Let's calculate:
d = (Mean of Treatment - Mean of Control) / Pooled Standard Deviation
d = (74 - 69) / 15
d = 0.33
(Note: Pooled Standard Deviation is a bit tricky if the standard deviations of the control and treatment group are different. What’s important in the calculation is that there is a numerator and a denominator. The numerator is simply the difference in the means of the two groups. The denominator has to do with the spread in the data and the number of points in the sample. But it’s very easy to calculate using a spreadsheet or a computer program.)
Interpreting Effect Sizes
Now that we have calculated the effect size for our example, Cohen's guidelines help us interpret the results:
Small effect: 0.2
Medium effect: 0.5
Large effect: 0.8
In educational terms:
0.2 represents roughly a quarter letter grade improvement (C to C+)
0.5 suggests about half a letter grade improvement (C to B-)
0.8 or larger indicates nearly a full letter grade improvement (C to B or A-)
In our tutoring example, the 0.33 effect size translated to meaningful changes in grade distribution (See Figure 2):
Four fewer students each in F and D ranges
Three more students each in C and B ranges
Two additional students achieving A grades
However, these improvements didn't affect all students equally. Further analysis might reveal that struggling students showed larger gains (perhaps 0.4) while high-achieving students showed smaller improvements (perhaps 0.1). Or, it might be the other way around. This heterogeneity in treatment effects can help educators target interventions more effectively.
Conclusion
In educational research and practice, understanding effect sizes is crucial for making informed decisions. Our analysis of the tutoring program demonstrates why. While traditional statistical significance might tell us that the program "works," the effect size of 0.33 tells us exactly how much it works. This detailed understanding helps administrators make practical decisions about resource allocation and program continuation.
The visualization and grade distribution analysis also highlight an important lesson: small effect sizes can still be meaningful in educational contexts, but their impact should be viewed realistically and holistically. Our tutoring program didn't dramatically transform student performance – it didn't turn D students into A students – but it did provide a consistent, modest boost across the grade spectrum. This nuanced understanding, which only effect size analysis can provide, helps set realistic expectations and informs how we communicate program benefits to stakeholders. Rather than simply declaring the program "statistically significant," we can now say with precision that it helps the average student improve by about a quarter of a standard deviation, moving some students up by one grade level and helping others move from failing to passing. This concrete, practical interpretation is what makes effect sizes such a valuable tool in educational research and decision-making.
While we've focused on an educational example, the concept of effect sizes extends far beyond the classroom. Whether evaluating a new medical treatment's impact on patient outcomes, assessing the effectiveness of a marketing campaign on sales, or studying the influence of policy changes on social behavior, effect sizes provide the same crucial insight: not just whether an intervention works, but how much it works. This quantification of impact, combined with cost considerations and implementation feasibility, enables evidence-based decision-making across all fields where measuring the magnitude of change matters.
It's important to note that while we have used causal language throughout our discussion – speaking of the "effect" of tutoring on grades – the interpretation of these relationships as truly causal depends critically on study design. Without proper experimental controls or random assignment to treatment conditions, what we measure might be correlational rather than causal. A strong effect size in an observational study might reflect not just the impact of the intervention, but also other factors like student motivation or family support. This caveat reminds us that effect sizes must always be interpreted within the context of the study's methodology and design.
Ellis, P. D. (2010). The essential guide to effect sizes: Statistical power, meta-analysis, and the interpretation of research results. Cambridge University Press. (p. xiii)